Polárkoordinátás deriváltak
A görbéket megadhatjuk polárkoordinátákat tartalmazó egyenletekkel is.
A közönséges derékszögű koordinátarendszerben egy pont helyzetét a vízszintes koordinátatengelyen mért x és a függőleges koordinátatengelyen mért y értékekkel adjuk meg.
A polárkoordinátás megadásnál ezzel szemben egy r és egy θ értéket használunk, ahol r
az origótól mért távolság, θ pedig az x-tengely pozitív félegyenese és az origóból a pontba mutató egyenes által bezárt szög.
A polárkoordinátákról a derékszögű koordinátákra a következőképpen térhetünk át: x = r cosθ és y = r sinθ.
Egy görbét pedig az r = f (θ) képlettel adhatunk meg (azaz r a θ függvénye).
Ha az y deriváltjait x függvényében szeretnénk megkapni ennél a görbénél,
átírhatjuk a képletét paraméteres egyenletekre, majd alkalmazhatjuk a paraméteres deriválással kapcsolatos képleteket.
Másként fogalmazva, ha r = f (θ), akkor x(θ) = r cosθ = f (θ)cosθ és y = r sinθ = f (θ)sinθ.
Ezzel a következő deriválási képletekhez jutunk:
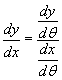 és
és 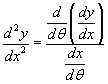 .
.
Ez teljesen hasonló a paraméteres esethez, csak épp a paraméterünket most θ-nak nevezzük és nem t-nek.
Próbálja ki a következőket:
- Az első applet egy kört mutat, amit igen egyszerűen az r = 1-gyel adunk meg (ha a kör alakja elnyúlt, kattintson az Equalize Axes gombra).
Az appletben th-t használunk θ helyett, hogy könnyebb legyen begépelni.
Mozgassa a th csúszkát, megváltoztatva ezzel θ értékét!
A polárkoordinátás megadásnál θ az x-tengely pozitív félegyenese és az origóból a pontba mutató (az ábrán szaggatott lilával jelzett) egyenes által bezárt szög.
Tehát θ az x-tengely pozitív félegyenese és a szaggatott lila egyenes közti szög.
Figyelje meg, hogy a polárkoordinátás egyenletünknél ahogyan θ változásával a lila pont befutja a polárkoordinátás görbét, az origótól való távolsága,
vagyis r mindig 1, minden θ értékre.
A polárkoordinátás egyenletünk paraméteres alakját az x(θ) = cosθ és y(θ) = sinθ egyenletek adják,
így a derivált
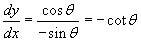 , ami összhangban van azzal,
amit a kör paraméteres deriválásánál kaptunk.
, ami összhangban van azzal,
amit a kör paraméteres deriválásánál kaptunk.
- Válassza ki a második példát a legördülő menüből, mely az r = θ spirált mutatja!
Mozgassa a th csúszkát, megváltoztatva θ értékét, és figyelje meg, mi történik r-rel.
Ha θ nő, r is nő, vagyis amíg θ egy teljes kört leír, a pont egyre távolodik az origótól.
A paraméteres egyenletek az x(θ) = θcosθ és y(θ) = θsinθ,
vagyis a derivált
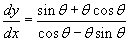 . Az eredmény a szorzási szabály miatt ilyen bonyolult.
. Az eredmény a szorzási szabály miatt ilyen bonyolult.
- Válassza ki a harmadik példát! Ez ugyanaz a spirál, csak most tmin = -6.28, így θ negatív értékeket is felvehet.
Tolja el a th csúszkát úgy, hogy θ negatív tartományba kerüljön, és figyelje, mi történik.
Mennyi r értéke ebben az esetben? Mit jelent a negatív r?
Mint látja, a negatív r azt jelenti, hogy a pont r távolságra van az origótól,
de most a θ meghatározásánál használt félegyenes ellentétes oldalára kerül.
Azzal, hogy r negatív is lehet, a polárkoordinátás egyenletek számos furcsa és szép görbét képesek leírni.
- Válassza ki a negyedik példát, mely egy négy szirmú rózsát mutat, az r = 3sin2θ képlettel megadva!
Mozgassa a th csúszkát és figyelje meg, r mely szirmoknál pozitív, melyeknél negatív.
A paraméteres egyenletek az x(θ) = 3sin2θcosθ és y(θ) = 3sin2θsinθ,
így a derivált
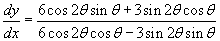 .
Ha akarja, megváltoztathatja a függvényképletben szereplő 3 és 2 értékeket más értékekre, és megnézheti, hogyan változtatja ez meg a rózsát.
Ha r = 3sin3θ, hányszor futjuk be a görbét a 0-tól 6.28-ig terjedő θ értéktartományban?
Ahogy növeli a szinusz függvényen belüli szorzót, úgy válik a görbe képe egyre durvábbá,
mivel a görbét egyre többször futjuk be. A görbét úgy teheti finomabb rajzolatúvá, hogy lecsökkenti
tmax értékét annyira, hogy csak egyszer fussuk be,
vagy pedig az intervallumokat megnöveli 1000-re, ezáltal a görbe több szegmensből fog felépülni, így a rajzolata is finomabb lesz.
.
Ha akarja, megváltoztathatja a függvényképletben szereplő 3 és 2 értékeket más értékekre, és megnézheti, hogyan változtatja ez meg a rózsát.
Ha r = 3sin3θ, hányszor futjuk be a görbét a 0-tól 6.28-ig terjedő θ értéktartományban?
Ahogy növeli a szinusz függvényen belüli szorzót, úgy válik a görbe képe egyre durvábbá,
mivel a görbét egyre többször futjuk be. A görbét úgy teheti finomabb rajzolatúvá, hogy lecsökkenti
tmax értékét annyira, hogy csak egyszer fussuk be,
vagy pedig az intervallumokat megnöveli 1000-re, ezáltal a görbe több szegmensből fog felépülni, így a rajzolata is finomabb lesz.
- Válassza ki az ötödik példát! Ez egy Limaçon görbe, melynek képlete r = 1+2cosθ.
Ha akarja, megváltoztathatja a függvényképletben szereplő 1 és 2 értékeket más értékekre, és megnézheti, hogyan változik ezáltal a görbe alakja.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
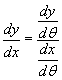 és
és 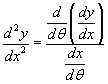 .
.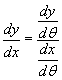 és
és 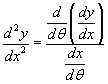 .
.