Hatványsorok és konvergencia intervallum
Az eddigiekben számsorozatokat és számsorokat vizsgáltunk. Amennyiben a sorozat elemei, melyeket összeadunk, hatványfüggvények, akkor hatványsorról beszélünk, melynek a definíciója 
. megjegyezzük, hogy a legtöbb tankönyvben n = 0-val kezdődik a sor 1 helyett, mivel a kitevőben n szerepel (ha n=1-el kezdődik, akkor a kitevőben (n - 1)-nek kellene megjelenni). Ugyancsak megemlítjük, hogy a c konstams értéket a hatványsor centrumának nevezzük. A hatványsorok az x függvényei és mindig konvergálni fognak x = c esetén, mivel ekkor a0 kivételével minden tag zérussá válik. Így a kérdés az, hogy a hatványsor x, c-től különböző értékeire konvergálni fog vagy nem. Használhatjuk a hányadoskritériumot, hogy megvizsgáljuk az abszolút konvergenciáját a hatványsornak, azaz vizsgáljuk két egymást követő tag abszolút értékének hányadosát, amint n tart a végtelenhez. Ha ez a határérték nem létezik, akkor a sor csak az x = c-ben konvergens. Ha a határérték zérus, akkor a sor minden x-re konvergens. Ha ez a határérték létezik és 
az alakja, akkor a sor konvergens, de csak a c körüli bizonyos intervallumon. Ezen utóbbi esetben R a konvergenciasugár és a sor konvergens, ha | x - c | < R. Mivel a hányadoskritérium alapján nem tudjuk eldönteni, vajon |x-c| = R esetén igaz-e a konvergencia, ezt a két esetet külön meg kell vizsgálni. A kapott x értékeket, amelyeken a sor konvergens konvergencia intervallum-nak nevezzük.
Próbálja ki a következőket!
- Az applet a következő hatványsort mutatja
Vegye észre, hogy a grafikonon csak Pnmax látható (ahol nmax vátoztatható), mivel egy végtelen sort kiszámolni végtelen ideig tartana! Azt is vegye észre, hogy ez az applet sum(var,start,end,expr) definíciót használ a hatványsor megadásához. A sum( ) művelet összeadja a sorozat elemeit, míg a var a neve annak a változónak, amelyre az összegzést végezzük (általában n), a start a kezdő érték, az end az utolsó érték (általában nmax ebben az appletben), és expr az általános elem képletete, amit összegezni kell. Ezt a következő matematikai alak mutatja 
. A hatványsorok esetében a kifejezés az n és az x fügvénye. Az appletben (x - c) a hatvány alapja, de ebben a példában c = 0. Tudjuk, hogy a mértani (geometriai) sor konvergens, ha a kvóciens -1 és 1 között van, azaz ez a sor konvergens, ha | x | < 1. Használhatjuk újra a hányadoskitériumot, hogy erről meggyőződjünk: 
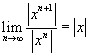, tehát a konvrgenciasugár 1. Ez azt jelenti, hogy a sor konvergens, ha | x | < 1. Ellenőriznünk kell még, hogy teljesül-e a konvergencia, ha | x | = 1 (azaz, ha x = 1 vagy, ha x = -1). Ahhoz, hogy ezt a konvergenciát ellenőrizzük, egyszerűen csak be kell helyetesíteni x helyére az adott értékeket és használni a kritériumot, ahogy ezt már tanultuk. Másképpen fogalmazva 
sor konvergens lesz-e vagy sem (és ugyanez a kérdés x = -1 esetére is). Mivel a hatvány alapja 1, ami konstans, nyilvánvalóan divegens lesz, mivel az n-edik tag nem tart zérushoz. Hasonlóan, ha az alalp -1, akkor alternáló sort kapunk, de a tagok nem lesznek kisebbek, 1 és -1 értékek váltakozva jelennek meg a sorban, tehát a sor itt sem lesz konvergens. Így tehát a konvergencia intervallum: | x | < 1. Tudja mozgatni az x csúszkát, amelynek következtében a fekete pont mozog a görbe mentén, jelzi, hogy amikor a konvergecia intervallumon kívül van x értéke, a pont a végtelenbe szalad. Ugyancsak tudja mozgatni a c csúszkát, figyelje mi történik, ha a konvergencia centrumát változtatja (és így könyebben megérti miért nevezzük ezt centrumnak).
- Nézzük a 2. példát a legördülő listáról, mely a
sort mutatja (ebben a példában c = 0 és nmax = 10 kezdetben). Használva újra a hányadoskriériumot, az előző példában elmondottak szerint, azt kapjuk, hogy az egymást követő tagok hányadosának határértéke 
, így a konvergenciasugár 3 lesz. Mivel ez is mértani sor, ahol a kvóciens x/3, a sor konvergálni fog, ha | x | < 3. A grafikonról látható, az x csúszka mozgatása során, hogy ez az erdemény elég jól megfelel a grafikonon látható fekete pont mozgásának (azért nem pontos a megfelelés, mert a grafikonon csak 10 tag összege szerepel a végtelen sok tag helyett.).
- Nézzük a 3. példát a legördülő listáról, mely a
sort mutaja. Megjegyezzük, hogy a kitevő itt bonyolultabb a kezelés szempontjából, mivel bizonyos tagok hiányoznak. Ha az összefüggésbe ezeket a tagokat is beírnánk oly módon, hogy az x kitevője n lenne, de a páratlan kitevőjű tagok zérusok lennének, akkor nem tudnánk alkalmazni a hányadoskritériumot. Használjuk a kritériumot a felírás szerinti általános elemre: 
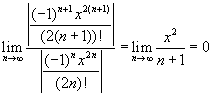. Mivel a határérték zérus, a sor konvergál minden x értékre. Tény, később látni fogjuk, hogy ez a sor a cos x függvény hatványsora. Amennyiben kicsinyíti a grafikont láthatja, hogy nem minden x-re konvergens. Ez annak a követezménye, hogy csak 10 tagig vettük az összeget. Mozgassa az nmax csúszkát és vegye észre, hogy a grafikon kisebb intervallumon fog konvergálni, amennyiben kisebb értékeket állít be! Hasonlóan, ha nmax nagyobb lesz, akkor egy nagyobb intervallumon fog konvergálni. Ha lehetőségünk lenne nmax értékének végtelent beállítani, akkor minden x értékre konvergens lenne.
- Nézzük a 4. példát, mely a
sort mutatja. Használjuk a hányadoskritériumot: 
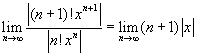. Mivel ez a határérték nem létezik, a sor csak az x = 0 esetén konvergens (amely ebben a példában a c). Ha beírja az nmax = 100 értéket, jobban fogja látni a grafikonon, hogy a konvergencia intervallum nagyon kicsi (figyelmeztetés: ne válasszon nmax értékének ennél nagyobbat, mert a programnak sok időre lesz szüksége, hogy kiszámolja).
This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.