Kalkulus Appletek

Taylor sorok és Taylor polinomok

Használni tudjuk a hatványsorokkal kapcsolatos ismereteinket arra, hogy olyan függvényt állítsunk elő velük, amelynek ugyanaz az értéke, mint egy másik függvénynek, és így véges számú tag figyelembevételével közelíthetjük az eredeti függvényt a konvergencia intervallumon belül. A Taylor sorok lehetőséget adnak arra, hogy ilyen sorokat adjunk meg: 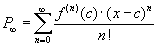, ahol f az a függvény amit hatványsorral szeretnénk megadni és 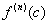az f függvény n-edik deriváltja a c helyen. Ha c = 0 a sort Maclaurin sornak szoktuk nevezni. Ahhoz, hogy megtaláljuk egy függvény polinom közelítését, használnunk kell a megadott összefüggést a kívánt n tagig, a végtelen helyett.

Próbálja ki a következőket!

1. Az applet a cos x függvény másodfokú polinomközelítését mutatja. A koszinusz függvény görbéje magenta színű, míg a Taylor polinom görbéje kék. Mozgassa az nmax csúszkát, növelje a polinom fokát és figyelje, hogy egyre jobban közelíti az eredeti függvényt a fokszám növelésével! A c csúszkát húzogatva figyelje meg mi történik a centrum megváloztatásakor! Ha c = 0 akkor a Maclaurin sor: 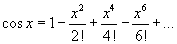. Használhatjuk a részösszegét a Maclaurin sornak, hogy ki tudjuk számolni a koszinusz értékét úgy, hogy csak összeadást, kivonást, szorzást és osztást használunk! Ha mozgatja az x csúszkát, a fekete pont a polinom görbe mentén mozog és a grafikon bal felső sarkában látja f értékét, a polinom értékét és a hibát (azaz, a különbség abszolút értékét).
   
   
2. Nézzük a 2. példát a legördülő listáról, amely a sin x függvény harmadfokú polinomközekítését mutatja! A Maclaurin sor 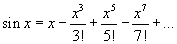. Mozgassa az nmax csúszkát, és figyelje meg, hogy egy magasabb fokú polinom egy jobb közelítést fog adni!
   
   
3. Nézzük a 3. példát, amely az exponenciális függvényt mutatja! Itt a Maclaurin sor:
   .
   
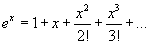
4. Nézzük a 4. példát, amely az 1/(1 - x) függvényt mutatja! Vegye észre, hogy ebben az esetben a konvergencia itervallumba most nem tartozik bele minden valós szám, a konvergencia intervallum sugara 1. A Maclaurin sor 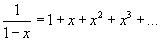, amely egy mértani sor. Mozgassa az nmax csúszkát és figyelje, hogy a konvergencia intervallum egyre kisebb lesz! Erre a példára nmax csúszkája 6 -ra van limitálva. Az olyan függvényekre, amelyek deriváltja nem túl bonyolult (mint a szinusz és a koszinusz), válaszhatunk nmax-nak olyan nagy értéket, amilyet akarunk. Azokra a függvényekre, amlyeknél az egymást követő deriváltak egyre bonyolultabbak lesznek (mint az 1/(1-x), tan x, stb.), a program gyorsan elakad a magasabb rendű deriváltak kiszámításában. Így ezekben az esetekben az a legjobb, ha limitáljuk nmax értékét 6-ra. Megjegyezzük még, hogy a sor a hiperbolának csak a baloldali részét közelíti. Amennyiben a jobboldali részét szeretnénk közelíteni, c > 1 választásra van szükség.
   
   
5. Próbálja ki saját feladatát, be kell írni a Taylor polinomot egy f függvényt és a c értékét! Ne legyen nmax > 6, ha a függvény magasabb deriváltjai egyre bonyolultabbak lesznek! Ki lehet próbálni az f (x) = ln(x) függvényt, vagy egy másodfokú polinomfüggvényt, mint az f (x) = x² - x - 1. Mit gondol a logaritmus függvény esetében mit kell tennie c-vel? A polinomfüggvénynél melyik nmax esetében lesz eltérés? Mekkora c értéke?

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.