Második derivált
Mivel egy függvény deriváltja egy másik függvény, ezért ennek is vehetjük a deriváltját, amit
második deriváltnak hívunk. Ha y = f (x), akkor a második deriváltat jelölhetjük
f '' (x)-el vagy 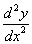 -el. Lehet magasabb deriváltakat is definiálni.
Ha az első derivált a függvény változásának mértékéről tudósít, a második derivált
a változás változásának mértékéről ad felvilágosítást. Fizikában, ha s (t) egy részecske térbeli pozíciója
t időpontban, úgy s' (t) = v (t) a gyorsaságot
(azaz a pozíció változásának a mértékét), v' (t)
= s'' (t) = a (t) pedig a gyorsulást (azaz a gyorsaság változásának a mértékét) fejezi ki.
-el. Lehet magasabb deriváltakat is definiálni.
Ha az első derivált a függvény változásának mértékéről tudósít, a második derivált
a változás változásának mértékéről ad felvilágosítást. Fizikában, ha s (t) egy részecske térbeli pozíciója
t időpontban, úgy s' (t) = v (t) a gyorsaságot
(azaz a pozíció változásának a mértékét), v' (t)
= s'' (t) = a (t) pedig a gyorsulást (azaz a gyorsaság változásának a mértékét) fejezi ki.
Próbálja ki a következőket:
- Az első példa egy köbfüggvényt mutat a baloldalon, a deriváltja középen látható, a második deriváltja pedig
a jobboldalon. A piros egyenes a köbfüggvény görbéjének az érintője, a görbe meredeksége a derivált értéke.
Mozgassa a csúszkát és hasonlítsa össze a piros egyenest a középső grafikonon látható piros célkereszttel!
Ahogy a piros érintő meredeksége egyre nagyobb pozitív érték, úgy kerül a célkereszt egyre magasabbra.
Amikor pedig a piros egyenes meredeksége csökken, a célkereszt is lejjebb kerül.
- A középső grafikon zöld egyenese a derivált függvény görbéjének az érintője, így a jobboldali grafikon zöld célkeresztje
a zöld egyenes meredekségének az értékét mutatja, vagyis ez lesz a második derivált (a derivált deriváltja).
Mozgassa a csúszkát és figyelje meg, hogy amikor a zöld egyenes meredeksége pozitív, akkor a második derivált is pozitív,
amikor pedig a zöld egyenes meredeksége negatív, a második derivált is negatív!
- A csúszka mozgatása közben észrevesz-e valamit, ami a második deriváltat a köbfüggvény grafikonjával összeköti?
Amikor a második derivált pozitív, milyen alakú a köbfüggvény grafikonja azon a tartományon? Amikor a második derivált negatív, milyen
alakú a köbfüggvény grafikonja? Azt fogja találni, hogy amikor a második derivált pozitív, a köbfüggvény grafikonja
konvex (azaz ilyen:
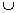 ), amikor pedig a második derivált negatív, a köbfüggvény grafikonja konkáv (azaz ilyen:
), amikor pedig a második derivált negatív, a köbfüggvény grafikonja konkáv (azaz ilyen:  ).
).
- Válassza ki a második példát a legördülő menüből! Ez egy szinuszgörbe. Mozgassa a csúszkát!
Látja, hogyan viszonyul egymáshoz a szinuszgörbe, a görbe deriváltja és a
második derivált? Ahogy a piros érintő mozog, nem úgy mutatja-e a piros célkereszt magassága a meredekségét?
Ahogy a zöld érintő mozog, nem úgy mutatja-e a zöld célkereszt magassága a meredekségét? És mit mond a második derivált
grafikonja a szinuszgörbe konvexitásáról?
- Válassza ki a harmadik példát, egy exponenciális függvényt! Mozgassa a csúszkát!
Mit jelent az, hogy a második derivált mindig pozitív? Miért?
Mit mond a második derivált pozitivitása az eredeti függvény alakjáról?
- Válassza ki a negyedik példát, egy hiperbolát! Teremtsen kapcsolatot a baloldali hiperbola konvexitása és a jobboldalon látható második derivált grafikonja között!
- Ön is megadhat tetszőleges függvényt a "f(x)=" mezőbe beírva a képletét, hogy megvizsgálja a
deriváltját és a második deriváltját.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
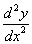 -el. Lehet magasabb deriváltakat is definiálni.
Ha az első derivált a függvény változásának mértékéről tudósít, a második derivált
a változás változásának mértékéről ad felvilágosítást. Fizikában, ha s (t) egy részecske térbeli pozíciója
t időpontban, úgy s' (t) = v (t) a gyorsaságot
(azaz a pozíció változásának a mértékét), v' (t)
= s'' (t) = a (t) pedig a gyorsulást (azaz a gyorsaság változásának a mértékét) fejezi ki.
-el. Lehet magasabb deriváltakat is definiálni.
Ha az első derivált a függvény változásának mértékéről tudósít, a második derivált
a változás változásának mértékéről ad felvilágosítást. Fizikában, ha s (t) egy részecske térbeli pozíciója
t időpontban, úgy s' (t) = v (t) a gyorsaságot
(azaz a pozíció változásának a mértékét), v' (t)
= s'' (t) = a (t) pedig a gyorsulást (azaz a gyorsaság változásának a mértékét) fejezi ki. 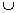 ), amikor pedig a második derivált negatív, a köbfüggvény grafikonja konkáv (azaz ilyen:
), amikor pedig a második derivált negatív, a köbfüggvény grafikonja konkáv (azaz ilyen:  ).
).